Les fractales font incontestablement partie des objets mathématiques les plus fascinants qui soient. Découverts en 1974 par le mathématicien français Benoît Mandelbrot, ces objets sont caractérisés notamment par le fait qu’ils sont autosimilaires, ce qui signifie que quelle que soit l’échelle à laquelle on les observe, leur aspect ne change pas (regarder cette vidéo pour visualiser un exemple… terrifiant si l’on lit les commentaires des internautes). Parmi les fractales les plus connues, on peut citer le flocon de Koch, le triangle de Sierpinski, ou encore les ensembles de Mandelbrot et de Julia.

De gauche à droite : le flocon de Koch, le triangle de Sierpinski, l’ensemble de Mandelbrot.
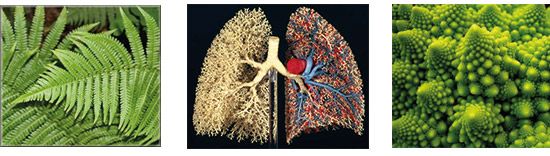
De façon spectaculaire, on retrouve également ces objets partout dans la nature lorsqu’on observe une fougère, certains aliments, des alvéoles pulmonaires, le cours de la bourse, ou les côtes bretonnes.
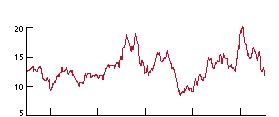
Il n’est pas possible de savoir si le cours de la bourse (ci-dessous) est sur une seconde, une minute, une journée, une année, un siècle : son évolution se comporte comme une fractale.
Au-delà de leur aspect tout à fait intrigant, ces objets présentent des particularités dont voici une sélection non exhaustive.
1. Les fractales ont révolutionné PIXAR
Le caractère autosimilaire des fractales est très perturbant pour l’esprit humain. On sait par exemple que si l’on mettait bout à bout l’ensemble des vaisseaux sanguins d’un adulte, on atteindrait une longueur d’environ 100 000 km, soit plus de deux fois le tour complet de la Terre ! Et pourtant, le réseau capillaire sanguin humain tient bel et bien dans le corps humain. Ce tour de passe-passe est lié au caractère autosimilaire du réseau. On comprend alors aisément qu’il est très difficile de dessiner une fractale à la main sans s’arracher les cheveux (comment dessiner 100 000 km de vaisseaux sanguins dans une surface aussi réduite que celle du corps humain ?) Et paradoxalement, ce caractère autosimilaire est très facile à mettre en œuvre algorithmiquement, à l’aide du principe de récurrence. Grâce à une simple formule, à une ligne de code, on peut générer à l’aide d’un ordinateur des objets aussi granuleux que l’on souhaite, avec un nombre minimum de paramètres, et une puissance de calcul moindre. Lorsque Pixar a découvert la puissance de ce concept, ils ont pu dessiner numériquement des paysages avec une précision et une finesse remarquable. La prochaine fois que vous regardez Toy Story, n’oubliez pas de rendre hommage à Benoît Mandelbrot !

Quelques lignes de code sont suffisantes pour générer le dessin lunaire ci-dessus (Source).
2. Les côtes bretonnes ont une structure de fractale
Lorsque vous vous promenez le long des côtes bretonnes, vous-êtes-vous déjà demandé quelle était la distance totale de la rive ? Figurez-vous qu’il s’agit là du question étonnamment complexe. La preuve, cette longueur a constamment évolué dans les manuels. Cela dépend en effet de l’échelle cartographique utilisée (et donc de l’unité de mesure considérée).
Ainsi, si l’unité de mesure est de 500 km, on obtient une longueur de 2 600 km, alors que si l’on prend une unité de 100 km, la distance augmente de 1200 km. Et pour un pas de 54 km, la côte mesure 5 570 km ; pour un pas de 17 km, 8 640 km et ainsi de suite, soit plus que la distance entre Paris et New-York… si l’on continuait à réduire le pas, on trouverait une longueur tendant vers l’infini ! Cette propriété intrigante des côtes bretonnes est intimement liée à son caractère fractal : plus on zoome, plus le rivage est irrégulier, granuleux, complexe, et donc difficile à mesurer. Lorsque l’on effectue les mesures avec un pas donné, on néglige nécessairement toutes les irrégularités qui sont plus fines que ce pas de mesure. Et lorsqu’il s’agit d’une fractale, l’erreur que l’on commet en omettant ces irrégularités tend vers l’infini.
Bien sûr, ce paradoxe n’est pas propre à la Bretagne. On observe ce même phénomène sur de nombreuses autres côtes qui ont été percutées pendant longtemps par des grosses vagues, par exemple en Angleterre.
La prochaine fois que vous trempez les pieds dans l’eau à Ouessant, n’oubliez pas de boire un cidre à la santé de Benoît Mandelbrot !
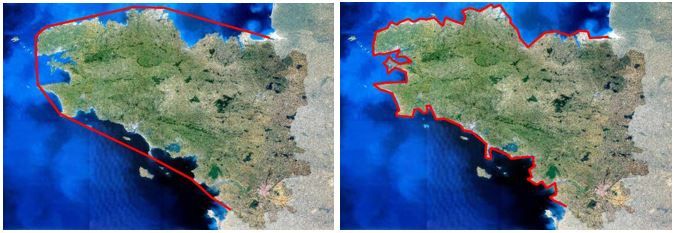
Calcul de la côte bretonne avec deux unités de mesure différentes.
3. Les fractales peuvent naître du chaos
Les amateurs de billard connaissent peut-être le jeu du chaos. Pour les autres, un petit rappel : considérez un triangle, et placez une boule n’importe où à l’intérieur de ce triangle. Tel un joueur de billard, si vous tapez dans la boule dans la direction d’un des coins du triangle, et que la boule parcourt la moitié (ou n’importe quelle fraction) de la distance entre sa position et le coin, vous observerez que la suite des trajectoires finira inévitablement par dessiner une fractale. Ceci est véritablement incroyable. A partir d’une séquence de mouvements chaotiques nait une structure ordonnée et complexe. Ce petit jeu a fasciné les mathématiciens avant que Benoît Mandelbrot n’élucide à nouveau le mystère. On sait aujourd’hui que l’on peut dessiner de très nombreuses fractales de cette manière. Ainsi, le triangle de Sierpinski ci-dessous peut être généré de manière déterministe (par récurrence) ou de manière aléatoire (par le chaos). Sacré Benoît !

Illustration en vidéo
La liste des particularités des fractales est bien plus longue, et il faudrait bien plus que quelques lignes pour en faire le tour. Nous verrons peut être dans un prochain billet que par exemple, les fractales permettent de faire de la data science, de la finance, de l’électronique, qu’elles ne sont ni en 2D, ni en 3D…mais quelque part entre les 2 ! Les fractales sont à la croisée des chemins entre les mathématiques, la géométrie, le dessin et la science-fiction. Sans aucun doute, elles n’ont pas fini de nous livrer tous leurs secrets.
Pour les curieux, Benoît Mandelbrot enseignait la théorie des fractales à l’université de Yale aux Etats-Unis, et l’intégralité des cours est disponible en ligne.
Découvrez également les pavages de Voronoï pour aller plus loin.
