Nous avons vu précédemment que les fractales sont des objets dotés de propriétés très particulières – notamment l’autosimilarité – et que l’on retrouve de telles structures partout dans la nature. Il arrive parfois que la fractale soit imbriquée au sein d’une autre structure tout aussi fascinante : le pavage de Voronoï.
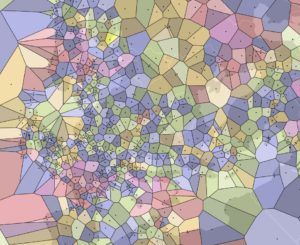
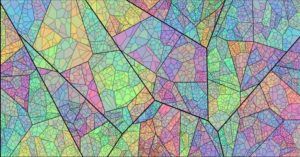
Exemples de pavages de Voronoï. Dans le second dessin, le pavage a également une structure fractale. (Source 1, Source 2)
Ces jolis dessins nous mettent la puce à l’oreille : ces structures semblent occuper l’espace intelligemment, et il n’est donc pas étonnant que l’on en retrouve un peu partout dans la nature.

(Source 1, Source 2)
1. Qu’est-ce qu’un pavage de Voronoï ?
Les pavages de Voronoï, formalisés par le mathématicien russe Georgi Voronoï (1868 – 1908), sont un découpage du plan en cellules à partir d’un ensemble discret de points appelés « germes ». Chaque cellule enferme un seul germe, et forme l’ensemble des points du plan plus proches de ce germe que d’aucun autre. Puisqu’une image vaut 1000 mots, en voici un exemple :
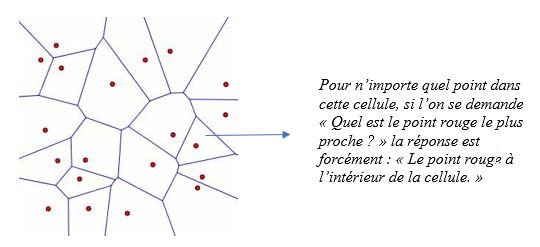
De manière plus intuitive, on peut dire qu’une cellule représente la « zone d’influence » du germe. Cliquez ici pour vous amuser à créer votre propre pavage de manière interactive.
Parmi toutes les propriétés intéressantes des pavages, on peut en retenir deux issues de la théorie des graphes: un pavage sur n germes a au plus 3n-5 arêtes (les segments en bleu) et 2n-6 sommets (les intersections des segments bleus).
2. Comment dessiner un tel pavage ?
Pour dessiner un pavage, il suffit de procéder comme suit :
a. Connecter chaque germe à ses plus proches voisins, formant un réseau de triangles (en vert ci-dessous)
b. Tracer toutes les médiatrices des segments obtenus (en rouge ci-dessous)
c. Relier toutes les intersections des médiatrices (en marron ci-dessous)

(Source)
Il peut être un peu fastidieux de dessiner un pavage manuellement, mais de nombreux algorithmes très efficaces existent pour les tracer de manière automatique. D’ailleurs, il est intéressant que ces structures riches soient si peu gourmandes d’un point de vue calculatoire et peuvent être tracées très rapidement. Si l’on cherche le pavage associé à n points, de l’ordre de nlog(n) opérations élémentaires sont suffisantes pour tracer le pavage complet (avec, par exemple, une stratégie « diviser pour régner« ).
3. Quelques applications
Historiquement, un demi-siècle avant la théorie newtonienne de la gravitation, Descartes (1644) utilisa ces structures afin de modéliser l’interaction gravitationnelle entre les étoiles. Plus de deux siècles plus tard, au cours d’un long hiver à Londres, le médecin John Snow (1813-1858) utilisa ces pavages afin de déterminer l’origine d’une épidémie de choléra : en construisant le diagramme des fontaines publiques et en dénombrant le nombre de malades dans chaque cellule, il put localiser l’origine de l’épidémie.
Les pavages de Voronoï sont de beaux objets mathématiques, derrière lesquels se cache beaucoup d’information. Les mathématiciens aiment ce genre d’objets et il n’est pas étonnant qu’ils se soient avérés séduisants pour l’optimisation et la science des données. Voyons quelques exemples.
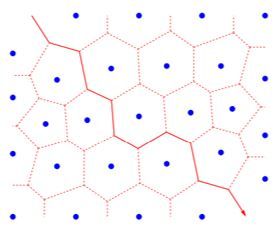
- Imaginez qu’un robot soit envoyé dans un champ de mines pour aller récupérer un objet. Les positions des mines sont connues, et pour minimiser le risque d’explosion, le robot doit circuler à chaque instant le plus loin possible d’elles. Pour déterminer la trajectoire du robot, il suffit de tracer le pavage de Voronoï dont les germes sont les mines (en bleu ci-dessous), et de longer les frontières des cellules (en rouge ci-dessous).
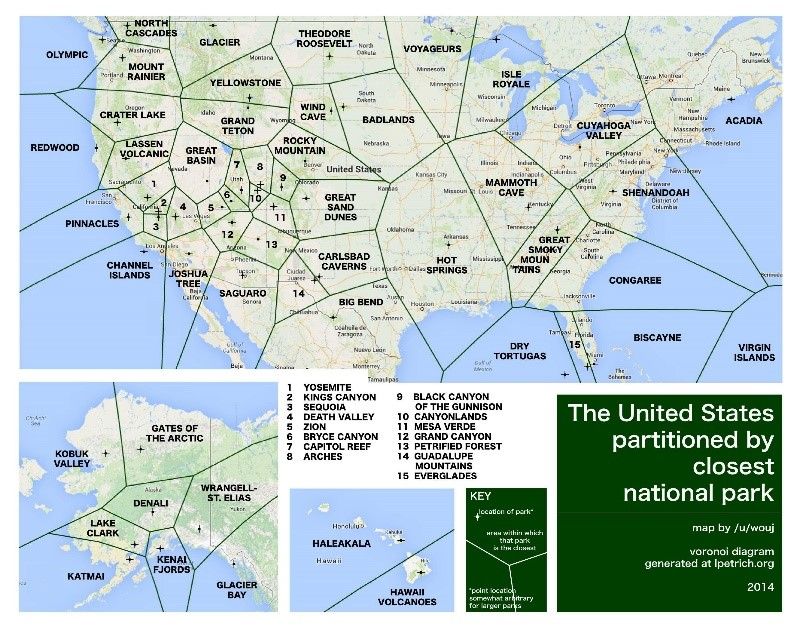
- Imaginez maintenant que vous faites du tourisme aux Etats-Unis. Vous voulez minimiser vos déplacements tout en couvrant un maximum de parc nationaux, vous souhaitez donc à tout moment connaître le parc national le proche de votre position. Pour cela, il suffit de tracer le pavage de Voronoï ayant pour germes les parcs nationaux américains. Easy !
(Source)
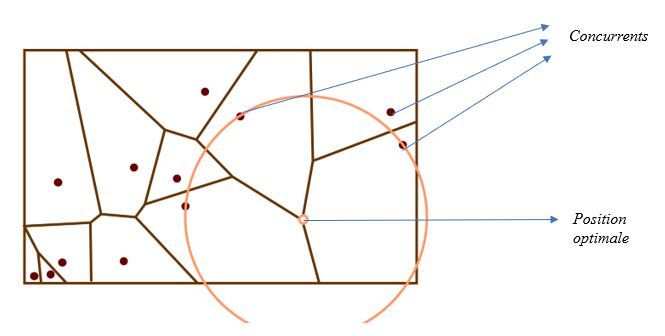
- Voici une application intéressante dans le domaine de la Supply-Chain, plus précisément en network design. Une entreprise souhaite ouvrir un magasin le plus loin possible de ses concurrents. Pour positionner le nouveau magasin, si à chaque concurrent correspond un germe, il suffit de trouver le cercle de plus grand rayon à l’intérieur duquel ne se trouve aucun germe (autrement dit le plus grand cercle vide). Le centre de ce cercle correspond alors à la localisation cherchée. Il est possible de trouver cette position en traçant le pavage de Voronoï dont les germes sont les concurrents ; celle-ci se situe typiquement à un croisement des frontières du pavage.
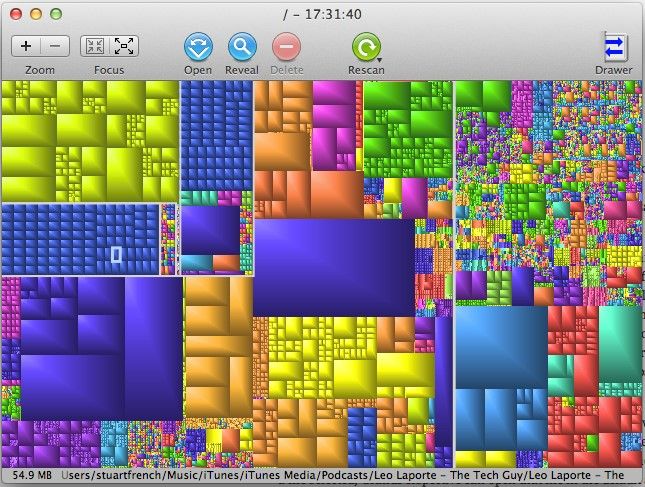
- Les pavages de Voronoï ont également une application intéressante pour les amateurs de Data Visualisation. Il est parfois commode de représenter de l’information sous forme de TreeMap (ou carte proportionnelle en français) pour hiérarchiser des données ; par exemple, pour représenter l’occupation du disque dur sur un ordinateur :
(Source)
Moins connu mais tout aussi utile, le Voronoï TreeMap permet de rendre compte de la distance entre les objets hiérarchisés. Par exemple, dans le diagramme ci-dessous sont organisés les pays du monde en fonction de leur continent, de leur population, et de leurs frontières communes.
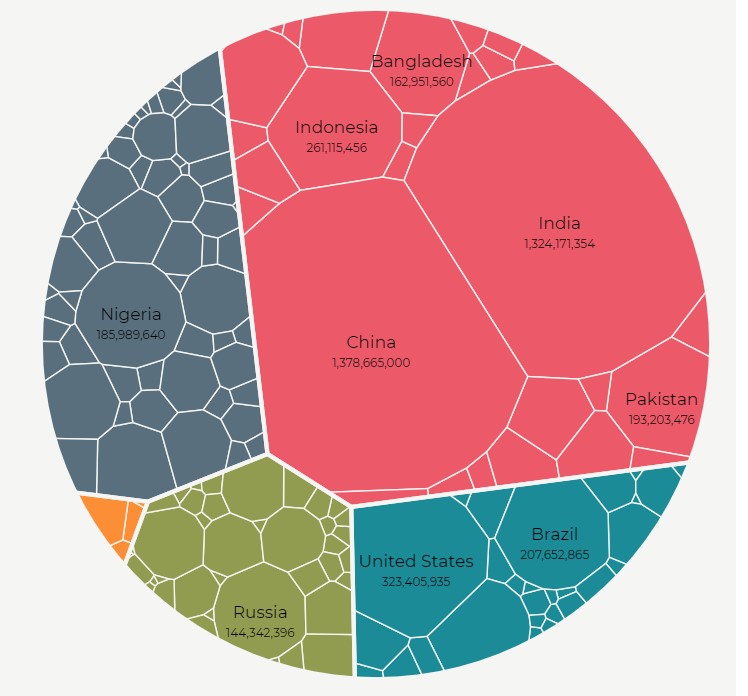 (Source)
(Source)Une dernière application bonus : Il est possible de résoudre certains problèmes d’optimisation en exploitant la structure du pavage, en étant très économe. Voyons un exemple géométrique. Supposons que parmi un ensemble de 1 000 points, on veuille trouver la paire de points la moins éloignée (en rouge ci-dessous).
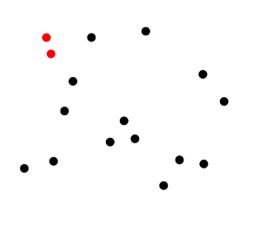 Une façon de faire consiste à calculer les distances entre toutes les paires de points, et de retenir la paire avec la distance minimale. Ceci requiert de l’ordre de 1 000² = 1 000 000 opérations élémentaires. Alors qu’en s’appuyant sur le pavage de Voronoï, on peut faire mieux ! Il suffit de déterminer la distance entre toute paire de points séparée par une arête du pavage (la frontière d’une cellule). Ce sont en effet les seules paires candidates, et cela ne requiert que de l’ordre de 1 000 opérations élémentaires (au plus 3n-5 [cf Section 1.]). Par conséquent, avec la seconde méthode, puisque la construction du pavage ne requière que 1000log(1000) = 3 000 opérations élémentaires, un total de l’ordre de 4 000 sont suffisantes. Qui dit mieux ?
Une façon de faire consiste à calculer les distances entre toutes les paires de points, et de retenir la paire avec la distance minimale. Ceci requiert de l’ordre de 1 000² = 1 000 000 opérations élémentaires. Alors qu’en s’appuyant sur le pavage de Voronoï, on peut faire mieux ! Il suffit de déterminer la distance entre toute paire de points séparée par une arête du pavage (la frontière d’une cellule). Ce sont en effet les seules paires candidates, et cela ne requiert que de l’ordre de 1 000 opérations élémentaires (au plus 3n-5 [cf Section 1.]). Par conséquent, avec la seconde méthode, puisque la construction du pavage ne requière que 1000log(1000) = 3 000 opérations élémentaires, un total de l’ordre de 4 000 sont suffisantes. Qui dit mieux ?
Conclusion
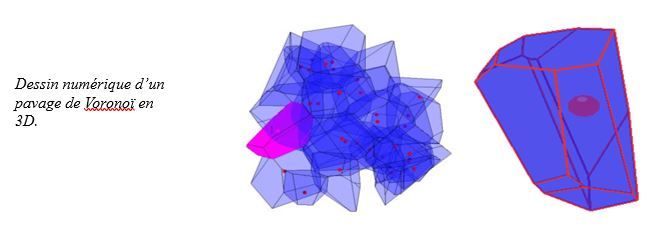
De nombreux articles scientifiques sont publiés chaque année dans lesquels ces diagrammes sont utilisés d’une façon ou d’une autre pour faire de l’optimisation. Les pavages de Voronoï sont des objets mathématiques fascinants qui illustrent bien que la frontière entre le dessin, l’optimisation et les mathématiques, est parfois très floue. Et bien sûr, on peut étendre ce principe à la 3D, et même à n dimensions, mais là, ça se complique un peu…